Question

At the end of each year, 10% interest is charged on a $500 loan. The interest applies to any unpaid balance on the loan, including previous interest.Select all the expressions that represent the loan balance after two years if no payments are made: 500+2⋅(0.1)⋅500500⋅(1.1)⋅(1.1)500+(0.1)+(0.1)500⋅(1.1)²(500+50)⋅(1.1)

Answer 1

The expressions that represent the loan balance after two years with no payments are
`\(500 \cdot (1.1)^2\) and \((500 + 50) \cdot (1.1)\).`

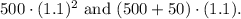
Step-by-step explanation:

The interest on the loan is compounded annually at a rate of 10%. The expression
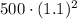`\(500 \cdot (1.1)^2\)` calculates the balance after two years, accounting for the 10% interest each year. Additionally,
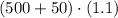`\((500 + 50) \cdot (1.1)\)`represents the balance after the first year with interest and then applies the 10% interest for the second year.

To break it down further,
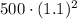`\(500 \cdot (1.1)^2\)` accounts for the initial loan amount of $500, compounded annually for two years. The term
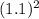`\((1.1)^2\)`represents the compounding effect of 10% interest for two years.

On the other hand,
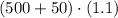`\((500 + 50) \cdot (1.1)\)` considers the balance after the first year, where $50 is the interest accrued. The term
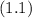`\((1.1)\)` then applies the additional 10% interest for the second year, resulting in the total balance after two years.

These expressions capture the compounding nature of the interest, reflecting the cumulative effect on the loan balance over the specified period.

In summary, the loan balance after two years, with no payments made, is accurately represented by the expressions
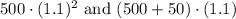`\(500 \cdot (1.1)^2\) and \((500 + 50) \cdot (1.1)\)`.

Answer 2

We have the following:

Since it's two years, the interest rate applies twice, just like that

`(500)\cdot(1.1)\cdot(1.1)=500\cdot(1.1)^2=605`

Now we check each case

`\begin{gathered} 500+2\cdot\mleft(0.1\mright)\cdot500=600 \\ \text{FALSE} \\ 500\cdot\mleft(1.1\mright)\cdot\mleft(1.1\mright)=605 \\ \text{TRUE} \\ 500+\mleft(0.1\mright)+\mleft(0.1\mright)=500.2 \\ \text{FALSE} \\ 500\cdot\mleft(1.1\mright)^(2)=605 \\ \text{TRUE } \\ \mleft(500+50\mright)\cdot\mleft(1.1\mright)=605 \\ \text{TRUE} \end{gathered}`