Answer:
• (x,y)=(2,2)
,
• Quadrant I
Step-by-step explanation:
Given the system of equations:
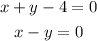
We are required to solve the system graphically.
To do this, find two points on each of the lines.
(a)x+y-4=0
When x=0
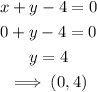
When x=1
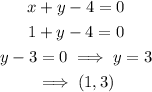
Join the points (0,4) and (1,3) to plot the first equation.
(b)x-y=0
When x=0, y=0 ==>(0,0)
When x=2, y=2 ==>(2,2)
Join the points (0,0) and (2,2) to plot the second equation.
The graph is shown below:
The two lines intersect at (2,2).
Therefore, the solution to the system of equations is:
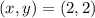
The solution (2,2) is in Quadrant I.