Question

Find an explicit rule for the nth term of the sequence.The second and fifth terms of a geometric sequence are 18 and 144, respectively.

Answer 1

Given:

second term = 18

fifth term = 144

The nth term of a geometric sequence is:

`\begin{gathered} a_n\text{ = ar}^(n-1) \\ Where\text{ a is the first term} \\ r\text{ is the common ratio} \end{gathered}`

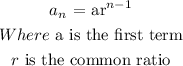
Hence, we have:

`\begin{gathered} \text{ar}^(2-1)\text{ = 18} \\ ar\text{ = 18} \\ \\ ar^(5-1)=\text{ 144} \\ ar^4\text{ =144} \end{gathered}`

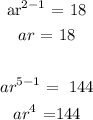
Divide the expression for the fifth term by the expression for the second term:

`\begin{gathered} (ar^4)/(ar)\text{ = }(144)/(18) \\ r^3\text{ = }(144)/(18) \\ r\text{ = 2} \end{gathered}`

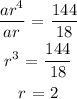
Substituting the value of r into any of the expression:

`\begin{gathered} ar\text{ = 18} \\ a\text{ }*\text{ 2 = 18} \\ Divide\text{ both sides by 2} \\ (2a)/(2)\text{ =}(18)/(2) \\ a\text{ = 9} \end{gathered}`

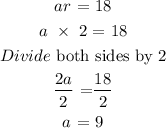
Hence, the explicit rule for the sequence is:

`a_n\text{ = 9\lparen2\rparen}^(n-1)`