Question

Let f(x) = x ^ (6x) Use logarithmic differentiation to determine the derivative.

Answer 1

The given function is:

`f(x)=x^(6x)`

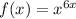
Rewrite the function in terms of y:

`y=x^(6x)`

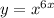
The derivative using logarithmic differentiation is done as follows:

`\begin{gathered} \ln y=\ln x^(6x) \\ \ln y=6x\ln x \end{gathered}`

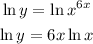
Differentiate both sides:

`(y^(\prime))/(y)=6x((1)/(x))+6\ln x`

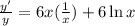
This is simplified to give:

`y^(\prime)=y(6+6\ln x)`

Substituting the value of y into the equation gives:

`y^(\prime)=x^(6x)(6+6\ln x)`

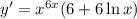
Therefore the derivative is:

`f^(\prime)(x)=6x^(6x)(\ln x+1)`

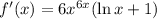
The value of f'(1) is:

`\begin{gathered} f^(\prime)(1)=6(1)^(6(1))(\ln1+1) \\ f^(\prime)(1)=6(1)(0+1) \\ f^(\prime)(1)=6 \end{gathered}`

Therefore it follows f'(x)=6