The equation is given below as
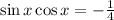
Recall that
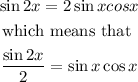
Therefore, equating the two-equation, we will have
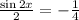
cross multiply, we will have
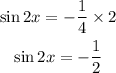
Therefore,
we will get the arc sign of both sides in radians to get
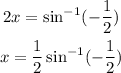
In radians, the final answer will be
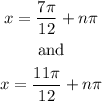
Therefore,
The finals answers are OPTION A and OPTION D