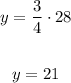Question

Suppose x varies directly with y. when x= 12, y = 9. what is y when x = 28?

Answer 1

Given :

x varies directly with y.

So, the relation between them will be :

`y=k\cdot x`

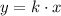
Where x is the constant of proportionality

Given x = 12 when y = 9 , the constant k will be :

`\begin{gathered} 9=k\cdot12 \\ k=(9)/(12)=(3)/(4) \end{gathered}`

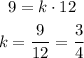
So, the relation will be :

`y=(3)/(4)x`

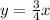
We need to find y when x = 28

So, substitute with x = 28

`\begin{gathered} y=(3)/(4)\cdot28 \\ \\ y=21 \end{gathered}`