Question

Which is better, an account paying 3.7% interest compoundedcontinuously or an account paying 3.75% compounded monthly

Answer 1

The rule of the interest compounded continuously is

`A=Pe^(rt)`

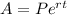
A is the new amount

P is the initial amount

r is the rate of interest in decimal

t is the time

The rule of the compounded monthly interest is

`A=P(1+(r)/(12))^(12t)`

A is the new amount

P is the initial amount

r is the interest rate in decimal

t is the time

Since the account pays 3.7% interest compounded continuously, then

`r=(3.7)/(100)=0.037`
`\begin{gathered} A=Pe^(0.037(1)) \\ A=P(1.037693021 \\ A=1.037693021P \end{gathered}`

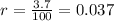
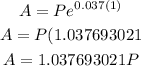
Since the other account pays 3.75% compounded monthly, then

`r=(3.75)/(100)=0.0375`
`\begin{gathered} A=P(1+(0.0375)/(12))^(12(1)) \\ A=P(1.038151293) \\ A=1.038151293P \end{gathered}`

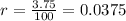
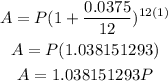
Since the value of A of the 2nd account is greater than the value of A in the 1st account, then

The better is the 2nd account