Given the table:
Day Value
1 20.71
2 19.69
3 19.61
4 19.64
5 19.26
Given that the table represents the closing prices of stock ABC, let's find the equation of the linear regression that fits the data.
Where:
n(number of data) = 5
Apply the slope intercept form of a linear equation:
y = mx + b
Where m is the slope and b is the y-intercept
Let's find the sum of the x-values (Days)
1 + 2 + 3 + 4 + 5 = 15
Also, sum up the y-values:
20.71 + 19.69 + 19.61 + 19.64 + 19.26 = 98.91
Sum of the products of the values of x and y.
We have:
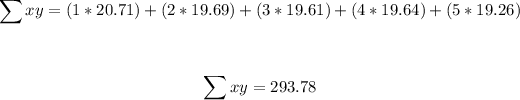
Sum up the values of the square of x
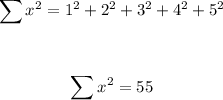
Sum up the values of the square of y:
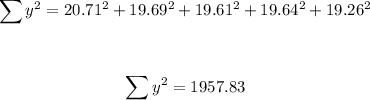
Let's find the slope, m:
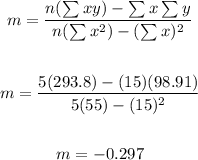
To find the y-intercept (b), apply the formula:
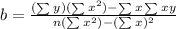
Thus, we have:
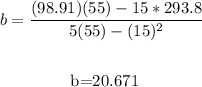
Substitute -0.297 for m and 20.671 for b in the slope-intercept form:
y = mx + b
Therefore, the equation of the linear regression for this data is:
y = -0.297x + 20.671
ANSWER:
C. y = -0.297x + 20.671