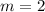1 Answer

Fdfrye · Answer 1 · 2023-02-19T20:46:02+0000

Given:

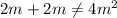
$2m+2m\\e4m^2$

Required:

We need to fin\gt\ht the value of m that proves that 2m + 2m is not equivalent to 4m^2.

Step-by-step explanation:

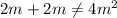
$2m+2m\\e4m^2$

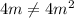
$4m\\e4m^2$

Substitute m =0 in the equation.

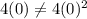
$4(0)\\e4(0)^2$
$0\\e0$

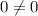
This is not true.

So m =0 does not prove that 2m + 2m is not equivalent to 4m^2

Substitute m =1 in the equaiton.

$4(1)\\e4(1)^2$
$4\\e4$

This is not true.

So m =1 does not prove that 2m + 2m is not equivalent to 4m^2

Substitute m =2 in the equaiton.

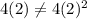
$4(2)\\e4(2)^2$

$8\\e16$

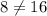
This is true.

So m =2 proves that 2m + 2m is not equivalent to 4m^2

Final answer:

Please log in or register to add a comment.