Question

9 × 10^5 is(A) ______times as larger as 3 ×10^3 5× 10^-3 is( B)______time as smaller as 5 × 10^-2

Answer 1

A) To know how many times greater 9*10⁵ is from 3*10³, you have to divide both values:

`(9\cdot10^5)/(3\cdot10^3)`

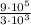
You can divide this fraction into two:

`(9)/(3)\cdot(10^5)/(10^3)`

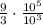
And solve them separatelly, afterwards you can multiply the results of both fractions:

`(9)/(3)=3`
`(10^5)/(10^3)=10^(5-3)=10^2`

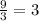
Note: when you divide two exponents values with the same base number, you have to subtract both exponent numbers.

Multiply both results:

`3\cdot10^2=300`

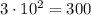
9*10⁵ is A. 300 times larger as 3*10³

B) To calculate how many times 5*10⁻³ is smaller than 5*10⁻², you have to divide the greater number by the smaller number.

`(5\cdot10^(-2))/(5\cdot10^(-3))`

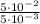
Following the same procedure as before:

`(5)/(5)\cdot(10^(-2))/(10^(-3))`
`(5)/(5)=1`

`(10^(-2))/(10^(-3))=10^(-2-(-3))=10^(-2+3)=10^1`

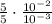
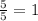
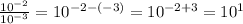
Reunite both values:

`1\cdot10^1=10`

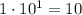
5*10⁻³ is B. 10 times smaller as 5*10⁻²