correctTo find the corresc answer, lets examine the following:
1° - the function has an asymptote at x = -2.
It means that the function can not be defined for x = -2.
For option a)
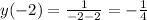
a) is defined, so it is wrong!
for option b)
![y(-2)=(2)/((-2)^2-4)=(2)/(4-4)=(2)/(0)=undefined]()
It can be b).
Lets analyse that x = 0 -> in a value positive between 1 and 2. For option b), we have:
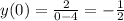
it is negative, and the expected value was positive.
b) is wrong!!
For c), lets analyze x = -2
![y(-2)=(3)/(-2+2)=(3)/(0)=\text{undefined}]()
Now anallyzing x = 0:
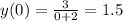
it is between 1 and 2, positive as we expected.
Lets check option d), for x = -2:
![f(-2)=-(3)/(2*(-2)+4)=-(3)/(0)=\text{undefined}]()
If we analyse it for x = 0, we have:
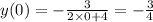
It is negative, and for this reason, different from the graph!
d) is wrong!
Analysing e) for x = -2
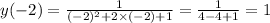
From the solution presented above, we are able to conclude that the correct answer is C)