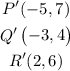Question

the vertices of a triangle are P(-5,-7), Q(-3,-4), and R(2,-6)what are the vertices of the image reflected across the x axis

Answer 1

By definition, a Reflection is a transformation in which the figure is flipped over a line of reflection.

When a figure is reflected across the x-axis, the rule you must apply is the following:

`(x,y)\rightarrow\mleft(x,-y\mright)`

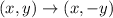
As you can notice, when a point is reflected across the x-axis, the sign of the y-coordinate changes.

In this case, you know that the vertices of the Pre-Image (the triangle PQR) are:

`\begin{gathered} P\mleft(-5,-7\mright);Q\mleft(-3,-4\mright);R\mleft(2,-6\mright) \\ \end{gathered}`

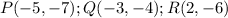
Then, applying the rule, you get that the vertices of the Image (triangle P'Q'R'), are:

`\begin{gathered} P\mleft(-5,-7\mright)\rightarrow P^(\prime)\mleft(-5,7\mright) \\ Q\mleft(-3,-4\mright)\rightarrow Q^(\prime)\begin{pmatrix}-3,4\end{pmatrix} \\ R\mleft(2,-6\mright)\rightarrow R^(\prime)\mleft(2,6\mright) \end{gathered}`

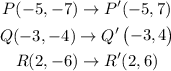
The answer is:

`\begin{gathered} P^(\prime)(-5,7) \\ Q^(\prime)\begin{pmatrix}-3,4\end{pmatrix} \\ R^(\prime)(2,6) \end{gathered}`