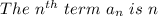Question

How do i find the nth term for the following sequence: 1,2,3,4,5,6,7,8,.. (Please explain in the easiest way possible I’m in foundation mathematics meaning I don’t understand it one bit)

Answer 1

Given the sequence;

`1,2,3,4,5,6,7,8,...`

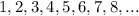
A sequence with a common difference d, is called an Arithmetic Sequence.

`\begin{gathered} a_n=n^{th\text{ }}term \\ \\ a_1=first\text{ }term=1 \\ \\ a_2=second\text{ t}erm=2 \\ \\ d=a_2-a_1 \\ \\ d=2-1 \end{gathered}`

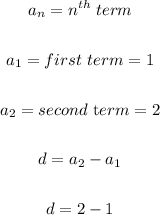
The nth term of an arithmetic sequence is generally given as;

`\begin{gathered} a_n=a_1+d(n-1) \\ Where\text{ }n\text{ }means\text{ }number\text{ }of\text{ }terms \end{gathered}`

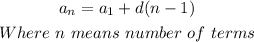
Thus, in the problem, the first term, the common difference are known. Then, we would substitute the value into the nth term formula. We have;

`a_n=1+1(n-1)`

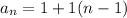
Then, simplify further;

`\begin{gathered} a_n=1+n-1 \\ a_n=1-1+n \\ a_n=n \end{gathered}`

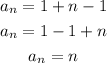
ANSWER:

`The\text{ }n^(th)\text{ }term\text{ }a_n\text{ }is\text{ }n`