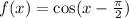Question

Which trigonometric function is equivalent to f(x) = sin x

Answer 1

Explanation

We are given the function:

`f(x)=\sin x`

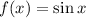
We are required to determine the equivalent trigonometric function as that given above.

We know that the following trigonometric equivalence exists:

`\begin{gathered} \cos(90-x)=\sin x \\ \cos(90+x)=-\sin x \\ \cos(180-x)=-\cos x \\ \cos(180+x)=-\cos x \\ \cos(270-x)=-\sin x \\ \cos(270+x)=\sin x \\ \cos(360-x)=\cos x \\ \cos(360+x)=\cos x \end{gathered}`

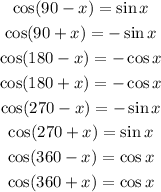
Next, we determine the value of each option as follows:

`\begin{gathered} Option\text{ }A:f(x)=\cos(x-(3\pi)/(2))=\cos\lbrace-((3\pi)/(2)-x)\rbrace \\ =\cos((3\pi)/(2)-x)=\cos(270-x)=-\sin x \\ \\ Option\text{ }B:f(x)=\cos(x-(\pi)/(2))=\cos\lbrace-((\pi)/(2)-x)\rbrace \\ =\cos((\pi)/(2)-x)=\cos(90-x)=\sin x \\ \\ Option\text{ }C:f(x)=\cos(-x-(\pi)/(2))=\cos\lbrace-((\pi)/(2)+x)\rbrace \\ =\cos((\pi)/(2)+x)=\cos(90+x)=-\sin x \\ \\ Option\text{ }D:f(x)=\cos(x+\pi)=\cos(180+x)=-\cos x \end{gathered}`

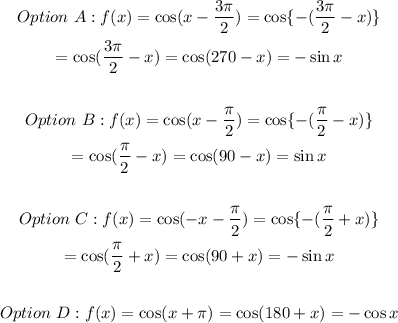
Hence, the answer is option B.

`\begin{equation*} f(x)=\cos(x-(\pi)/(2)) \end{equation*}`