Question

If the diameter of a circle is 6, find the exact area of a sector with a sector angle of π.

Answer 1

4.5pi square units

Step-by-step explanation:

Area of the sector is expressed as

`A\text{ =}(\theta)/(360)*\pi r^2`

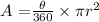
r is the radius of the circle

theta is the central angle

Given

theta = pi = 180 degrees

radius = diameter/2

radius = 6/2 = 3

Substitute the given values into the expression above;

`\begin{gathered} A\text{ = }(180)/(360)*\pi(3)^2 \\ A\text{ = }(1)/(2)*9\pi \\ A\text{ = }(9\pi)/(2) \\ A\text{ = 4.5}\pi units^2 \end{gathered}`

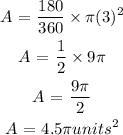
hence the area of the sector is 4.5pi square units