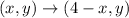How to write the rule for #11 if no rule describe the transformation in words.

Question

asked Sep 19, 2023 162k views

1 Answer

Harald Hoyer · Answer 1 · 2023-09-26T01:06:45+0000

Step-by-step explanation

Let's assume that we have points of the form (x,y). If those points are reflected about the line x=a then the reflected points are given by:

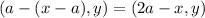
So for example if we have the points D=(1,1) and E=(0,-2) and we reflect them about the line x=2 we get:

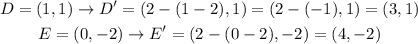
$\begin{gathered} D=(1,1)\rightarrow D^(\prime)=(2-(1-2),1)=(2-(-1),1)=(3,1) \\ E=(0,-2)\rightarrow E^(\prime)=(2-(0-2),-2)=(4,-2) \end{gathered}$

These points D' and E' are the same as those in the graph.

Answer

So the transformation performed in question 11 is a reflection about the line x=2 and it is described with this rule:

$(x,y)\rightarrow(4-x,y)$