Given:
Point O=(-3,-3)
Point P=(3,-7)
Point Q=(5,-4)
Point R=(-1,0)
To determine the slope, we use the formula:
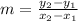
To get the slope of OP, we let :
x1=-3
y1=-3
x2=3
y2=-7
So,
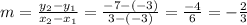
To get the length of OP, we use the distance formula:
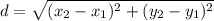
where:
d=distance
So,
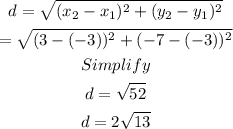
Hence, the length of OP is:
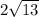
For PQ, we let:
x1=3
y1=-7
x2=5
y2=-4
So,
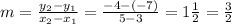
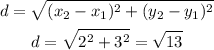
For QR, we let:
x1=5
y1=-4
x2=-1
y2=0
So,
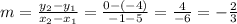
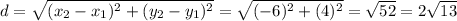
For RO, we let:
x1=-1
y1=0
x2=-3
y2=-3
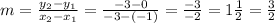
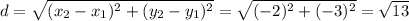
Therefore, the lengths are:
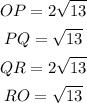
The given Quadrilateral OPQR is a rectangle since the opposite sides are equal and parallel to each other.