Solution:
Given:
In a circle, a radius perpendicular to a chord bisects the chord.

Hence, the right triangle can be extracted below.
To get the radius of the circle, we use the trigonometric identity of sine.
Hence,
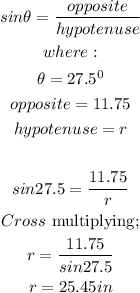
Therefore, the radius of the circle is 25.45 in