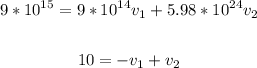Question

In a hypothetical situation, a meteorite of mass 9 x 10¹⁴ kg strikes earth with a velocity of 10m/s. Assume that the collision is elastic. Comment on the final velocities of earth and the meteorite.

Answer 1

Given:

Mass of meteorite = 9 x 10¹⁴ kg

Initial Velocity of meteorite = 10 m/s

Assuming that the collision is elastic, let's determine the final velocities of earth and meteorite.

Where:

Mass of earth = 5.98 x 10²⁴ kg

To determine the final velocity, apply the conservation of momentum

`m_1u_1+m_2u_2=m_1v_1+m_2v_2`

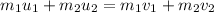
Where:

m1 = 9 x 10¹⁴ kg

m2 = 5.98 x 10²⁴ kg

u1 is the initial velocity of meteorite = 10 m/s

u2 is the initial velocity of the earth = 0 m/s (the earth at rest).

v1 is the final velocity of the meteorite

v2 is the final velocity of the earth.

Thus, we have:

`\begin{gathered} (9\ast10^(14)*10)+(5.98\ast10^(24)*0)=(9\ast10^(14)* v_1)+(5.98\ast10^(24)* v_2) \\ \\ 9\ast10^(15)=9\ast10^(14)v_1+5.98\ast10^(24)v_2 \end{gathered}`
`10=-v_1+v_2`

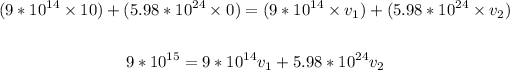
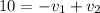
Now, let's solve the system of equations:

`\begin{gathered} 9\ast10^(15)=9\ast10^(14)v_1+5.98\ast10^(24)v_2 \\ \\ 10=-v_1+v_2 \end{gathered}`