To compare between slopes, we first have to calculate the value of the slope of the graph given using the following formula:

For this, we have to choose two points: (-3, 1), (-1, 3). Replacing the values we get:

Then, our slope is equal to 1.
Now, we have to calculate the slopes of the tables using the same formula and choosing 2 points.
• A
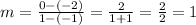
This option has the same slope as ours, then, it is not the answer.
• C

This is greater than our slope, then it is not the answer.
Also, option B has a greater slope as 5/2 = 2.5.
Finally, 1/4 = 0.25 is less than our slope.
Answer: D