Question

Why can't you solve for side b as your first step to this problem?

Answer 1

The triangle in the question can be solved using two rules

They are:

SINE RULE AND COSINE RULE

The sine rule states that

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

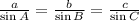
While the cosine rule is

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ b^2=a^2+c^2-2\text{ac}\cos B \\ c^2=a^2+b^2-2ab\cos C \end{gathered}`

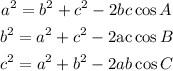
The given values in the question include

`\begin{gathered} a=8.4,A=26^0 \\ b=\text{?,B}=\text{?} \\ c=12.4,C=? \end{gathered}`

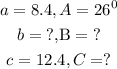
We cannot solve b as the first step in the question because the angle at B is not given

Step Instead, we will have to, first of all, use the sine rule below to get the angle at C

`(a)/(\sin A)=(c)/(\sin C)`

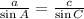
Substituting the values, we will have

`\begin{gathered} (a)/(\sin A)=(c)/(\sin C) \\ (8.4)/(\sin26^0)=(12.4)/(\sin C) \end{gathered}`

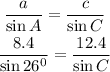
Cross multiply, we will have

`\begin{gathered} (8.4)/(\sin26^0)=(12.4)/(\sin C) \\ 8.4*\sin C=12.4*\sin 26^0 \\ 8.4\sin C=5.4358 \\ \text{divide both sides by 8.4} \\ (8.4\sin C)/(8.4)=(5.4358)/(8.4) \\ \sin C=0.6471 \\ C=\sin ^(-1)0.6471 \\ C=40.3^0 \end{gathered}`

Step 2: Calculate the value of angle B next using the sum of angles in a triangle=180°

`\begin{gathered} \angle A+\angle B+\angle C=180^0 \\ 26^0+\angle B+40.3^0=180^0 \\ 66.3^0+\angle B=180^0 \\ \angle B=180^0-66.3 \\ \angle B=113.7^0 \end{gathered}`

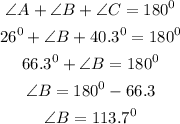
Step 3: Calculate the value of b using the the sine rule below

`(a)/(\sin A)=(b)/(\sin B)`

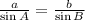
Substituting the value, we will have

`\begin{gathered} (a)/(\sin A)=(b)/(\sin B) \\ (8.4)/(\sin26^0)=(b)/(\sin113.7^0) \end{gathered}`

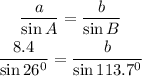
Cross multiply, we will have

`\begin{gathered} (8.4)/(\sin26^0)=(b)/(\sin113.7^0) \\ b*\sin 26=8.4*\sin 113.7^0 \\ b=(8.4*\sin 113.7)/(\sin 26^0) \\ b=17.5 \end{gathered}`

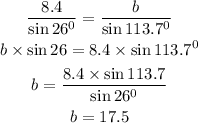
Therefore,

We cannot solve b as the first step because no side (b) or angle for B was given

We will have to calculate the value of Angle C(because the side at c was given) , followed by calculating the value of angle B using the sum of angles in a triangle (180) and then calculate the value of b using the sine rule (because the angle at B has been calculated)

The explanation of the solution is shown above