We have to solve the inequality
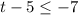
To do that, we add the 5 to both sides of the inequality, then we have
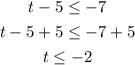
Then the solution to the inequality in interval notation is
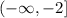
To graph the inequality we first graph the equation
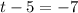
simplifying the equation we have
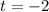
This represents a vertical line that intersects with -2
Now we have to decide wich of the two semiplanes we have to choose to "color" that represents the solution of the inequality, since the solution was
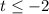
we color the semiplane to the left of the line