hello
we are going to solve this question via substitution method
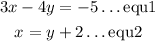
put equation 2 into equation 1
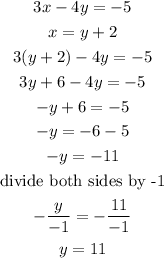
put y = 11 into equation 1 or 2
with equation 1
put y = 11
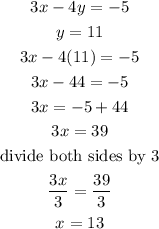
fro the calculations above, the solutions to the equations with the value of x and y are (13) and (11)