Question

The data in the table shows a sinusoidal relationship between the number of seconds an object has been moving and its velocity

v(x) , measured in centimeters per second.
please help

Answer 1

8

20

12

Explanation:

Answer 2

The period of the cosine function that models the data is 20 seconds, the midline is at
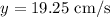`$y=19.25 \mathrm{~cm} / \mathrm{s}$`, and the amplitude is
`$15.25 \mathrm{~cm} / \mathrm{s}$`.

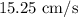The table shows a values for x and v(x), and it seems to illustrate a sinusoidal relationship between time in seconds and velocity in centimeters per second. The task is to determine the period and the midline equation of the cosine function that models the data.

Let's analyze the data to find the period and the midline of the cosine function:

1. Identifying the Period:

• The period of a sinusoidal function is the length of one complete cycle of the wave. We can find this by looking at the x-values at which the function starts repeating its pattern.
• From the given values, we can see that the velocity starts high, decreases to a low, and then increases back to the high. This indicates one complete cycle.

2. Calculating the Midline:

• The midline of a sinusoidal function is the horizontal line that runs exactly in the middle of the maximum and minimum values of the function. It represents the average value of the function.
• To calculate the midline, we take the average of the maximum and minimum values of v(x).

3. Determining the Amplitude:

• The amplitude is the measure of the function's displacement from the midline to the maximum or minimum. It is calculated as half the distance between the maximum and minimum values.

Let's start by plotting the given points to better visualize the data and determine the period and the midline. After plotting, we can perform the necessary calculations.

(Graph is given below)

The plot of the velocity v(x) over time x shows a sinusoidal pattern. To find the period, we look for the interval over which the pattern repeats. It appears that the function completes one full cycle between x=2 and x=22. Thus, the period would be x= 22-2=20 seconds.

For the midline, we need to calculate the average of the maximum and minimum values of v(x). The maximum value is at x=2, which is
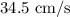`$34.5 \mathrm{~cm} / \mathrm{s}$`, and the minimum value is at x=16, which is
`$4 \mathrm{~cm} / \mathrm{s}$`.

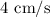Let's calculate the midline equation
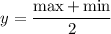`$y=(\max +\min )/(2)$` and the amplitude
`$A=(\max -\min )/(2)$`.

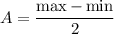The equation of the midline of the cosine function is
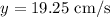`$y=19.25 \mathrm{~cm} / \mathrm{s}$`, and the amplitude of the cosine function is
`$15.25 \mathrm{~cm} / \mathrm{s}$`.

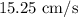Graph: