AB=15 AD=31 BC=31 CD=15
Step-by-step explanation
Step 1
the perimeter of the parallelogram ABCD is
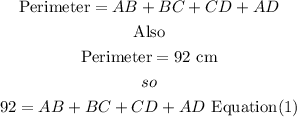
on a parallelogram, 2 length are similear

now, replace in equation (1)
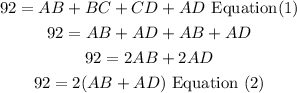
Step 2
now,AD is 1 cm more than twice AB, in other words, you have to add 1 to twice AB to ger AD
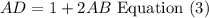
Step 3
solve equation (2) and (3)
replace equation (3) in equation(2)

Step 4
replace the value of AB in equation (3) to find AD
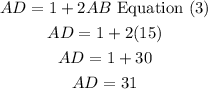
I hope this helps you