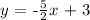ANSWER
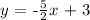
Explanation:
Given the following coordinate points (-4, 13) and (2, -2)
The standard form of the slope-intercept equation is written below
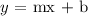
Where
m = slope of the line
b = intercept of the y-axis
The next thing is to find the slope
The formula for slope is given below as
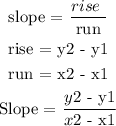
According to the given points, we can deduce the following
x1 = -4
y1 = 13
x2 = 2
y2 = -2
Substitute the following data into the above formula
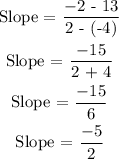
The slope-intercept form of a given point
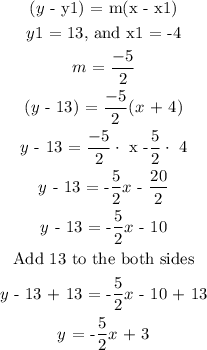
Hence, the equation of the coordinate point