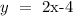1 Answer

Akoi Meexx · Answer 1 · 2023-06-19T08:29:30+0000

The equation is;

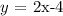
$y\text{ = 2x-4}$

Here, we want to write the equation given the table

From what we have,we need to understand the relationship between x and y

From what we can see, as there is an increase in x by a value of 1, there is an increase in y by 2 units

This shows a linear relationship

We can represent this relationship with a linear model

This is;

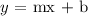
$y\text{ = mx + b}$

where m is the slope and b is the y-intercept

The value of b is the y-value when x = 0

As we can see, this is -4

So we have the partially complete equation as;

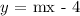
$y\text{ = mx - 4}$

what is left is to get m

Simply substitute any point in the equation

We can use the point (3,2)

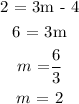
$\begin{gathered} 2\text{ = 3m - 4} \\ 6\text{ = 3m} \\ m\text{ =}(6)/(3) \\ m\text{ = 2} \end{gathered}$

The equation of the model is thus;

$y\text{ }=\text{ 2x-4}$

Please log in or register to add a comment.