The question provides that:
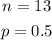
Therefore, we have that:
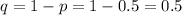
To check if we can use the normal distribution as an approximation, we will check the values of np and nq:
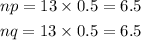
Since,
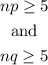
then we can use the normal distribution as an approximation.
To evaluate P (at least 10), we are evaluating:
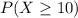
The standard deviation of the distribution is gotten to be:
![\sigma=\sqrt[]{np}=\sqrt[]{6.5}=2.550](https://img.qammunity.org/2023/formulas/mathematics/college/9s39s18hs13bvv1kl1v4x5otn5us37iwxo.png)
The mean is 6.5.
Therefore, the Z-score is gotten to be:
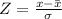
Hence, it is calculated to be:
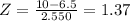
The probability is therefore given to be:
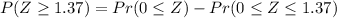
Using the Probability Distribution Table, we have:
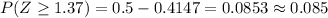
Therefore, the answer is:
