Question

If one line passes through the points (3,-5) and (1, 9). what must be the slope of a line perpendicular to it? Your answer

Answer 1

In order to find the slope of the perpendicular line, let's first find the slope of these two points.

We can find it using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

So, using the points (3, -5) and (1, 9), we have:

`m=(9-(-5))/(1-3)=(14)/(-2)=-7`

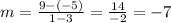
So the slope of this line is -7.

In order to find a perpendicular line, the slopes of the lines need to have the following relation:

`m_1=-(1)/(m_2)`

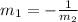
Using m1 = -7, we have:

`\begin{gathered} -7=-(1)/(m_2) \\ m_2=-(1)/(-7)=(1)/(7) \end{gathered}`

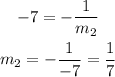
So the slope of the perpendicular line is 1/7.