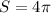1 Answer

Tim Bray · Answer 1 · 2023-02-20T02:45:58+0000

Given:

There are given the value of radius and the value of the angle in radian.

Step-by-step explanation:

To find the arc length, we need to use the formula of arc length.

So,

From the formula:

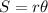
$S=r\theta$

Where,

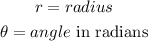
$\begin{gathered} r=radius \\ \theta=angle\text{ in radians} \end{gathered}$

So,

Put all the values into the above formula:

Then,

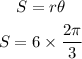
$\begin{gathered} S=r\theta \\ S=6*(2\pi)/(3) \end{gathered}$

Then,

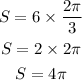
$\begin{gathered} S=6*(2\pi)/(3) \\ S=2*2\pi \\ S=4\pi \end{gathered}$

Final answer:

Hence, the value of arc length is shown below:

$S=4\pi$

Please log in or register to add a comment.