Let H and T denote and outcome of getting a head, or a tail, respectively.
Consider the experiment of tossing three coins.
The sample space will be defined as,
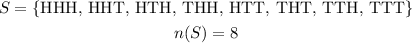
As per the given options, X is assumed to be the random variable representing the number of heads obtained in a particular outcome of the experiment.
Consider that the probability of any favourable event (F) is given by,
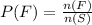
Consider the event of getting no head.
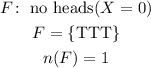
The corresponding probability is given by,
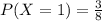
Consider the event of getting a head.
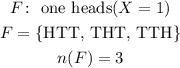
The corresponding probability is given by,
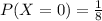
Thus, the probability of getting a head is,
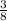
Consider the event of getting two head.
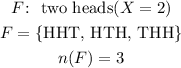
The corresponding probability is given by,
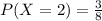
Consider the event of getting three head.
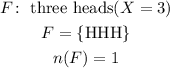
The corresponding probability is given by,
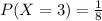
Use the values to create the probability distribution table as follows,
Therefore, the 3rd option denotes the correct probability distribution.