Notice that sin(x) is not a one-to-one function since
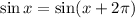
(The period of the sine function is 2pi)
On the other hand, a function needs to be one-to-one in order to be invertible.
Thus, the answer to the first gap is 'is not one-to-one'.
As for the second gap, notice that
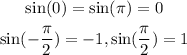
The maximum interval at which f(x) is one to one is
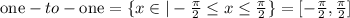
This is the maximum interval that verifies the horizontal-line test.
The answer to the second gap is [-pi/2,pi/2]
Notice that if the domain of the inverse function is [-1,1]; then the domain of such function is [-pi/2,pi/2]