Question

For the pair of points find the distance between them and the midpoint of the line segment joining them.(720,50), (125,18)The distance is(Simplify your answer. Type an exact answer, using radicals as needed.)The midpoint is(Simplify your answer. Type an ordered pair. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the

Answer 1

Given two points

`(x_1,y_1)`

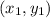
and

`(x_2,y_2)`

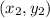
The distance between them is >>>

`D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

The points given are (Sqrt(20), Sqrt(50)) and (Sqrt(125), Sqrt(8)), so their distance is >>>

`\begin{gathered} D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ D=\sqrt[]{(\sqrt[]{8}-\sqrt[]{50})^2+(\sqrt[]{125}-\sqrt[]{20})^2} \\ D=\sqrt[]{(\sqrt8)^2-2(\sqrt[]{8})(\sqrt[]{50})+(\sqrt[]{50})^2^{}+(\sqrt[]{125})^2-2(\sqrt[]{125})(\sqrt[]{20})+(\sqrt[]{20})^2} \\ D=\sqrt[]{8-2(2\sqrt[]{2})(5\sqrt[]{2})+50+125-2(5\sqrt[]{5})(2\sqrt[]{5})+20} \\ D=\sqrt[]{8-40+50+125-100+20} \\ D=\sqrt[]{63} \\ D=3\sqrt[]{7} \end{gathered}`

----------------------------------------------------------------------------------------------------------

The midpoint formula is >>>

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

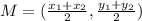
Plugging in the points, we have >>>

`\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ M=(\frac{\sqrt[]{20}+\sqrt[]{125}}{2},\frac{\sqrt[]{50}+\sqrt[]{8}}{2}) \\ M=(\frac{2\sqrt5+5\sqrt[]{5}}{2},\frac{5\sqrt[]{2}+2\sqrt[]{2}}{2}) \\ M=(\frac{7\sqrt[]{5}}{2},\frac{7\sqrt[]{2}}{2}) \end{gathered}`