Question

letter b from question 7, pleaseThe d om th ind th irous len A perpendicular passes through (2, 4) and meets a line at (3,-1), find the equation of the Find the equation of a line passing through (5, -6) perpendicular to: 2x + y = 12 (b) 3x + 5y = 7 (c) x + 3y = 8 (d) 7x - 12y = 5 (e) 2y = 5 (1) x = 7 5. Find the equation of the line connecting the points of intersection of; (a) Sr + y = 4 3.x - y = 12 and (b) Sy = x - 9x 2x = 6 y = - 6 x=1 (a) perpendicular (b) line and Sy=x - 9 A perpendicular from the origin meets a line at (4,-5), find the equation of the (a) perpendicular (b) line

Answer 1

As the first line passes through the origin, that is point (0,0) and the through the point (4,-5), you can find the slope of this line with the formula

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1),(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

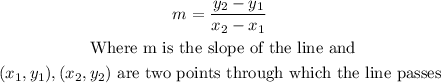
So, you have

`\begin{gathered} (x_1,y_1)=(0,0) \\ (x_2,y_2)=(4,-5) \\ m=(-5-0)/(4-0) \\ m=(-5)/(4) \end{gathered}`

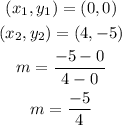
Now, you can use the point-slope formulas to find the equation of the line in its slope-intercept form

`\begin{gathered} y-y_1=m(x-x_1) \\ y-0_{}=(-5)/(4)(x-0) \\ y=(-5)/(4)x \end{gathered}`

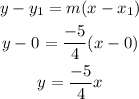
Therefore, the equation of the first line and the answer of numeral b) is

`y=(-5)/(4)x`

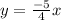
On the other hand, the slopes of perpendicular lines satisfy the following equation

`\begin{gathered} m_2=(-1)/(m_1) \\ \text{ Where }m_1\text{ is the slope of line 1 and} \\ m_2\text{ is the slope of line 2} \end{gathered}`

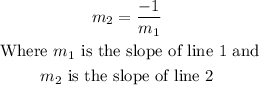
So, to find the equation of the second line that is perpendicular to the first, you can find its slope and then use the point-slope formula

`\begin{gathered} m_1=(-5)/(4)_{} \\ m_2=\frac{-1}{(-5)/(4)_{}} \\ m_2=\frac{(-1)/(1)}{(-5)/(4)_{}} \\ m_2=(-1\cdot4)/(1\cdot-5) \\ m_2=(4)/(5) \end{gathered}`

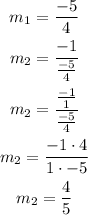
Now, using the point-slope formula with the point (4,-5)

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-5)_{}=(4)/(5)(x-4) \\ y+5_{}=(4)/(5)x-(16)/(5) \\ \text{ Subtract 5 from both sides of the equation} \\ y+5-5_{}=(4)/(5)x-(16)/(5)-5 \\ y=(4)/(5)x-(41)/(5) \end{gathered}`

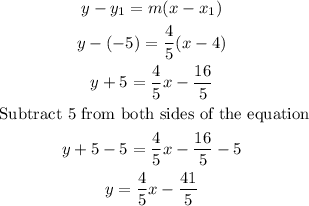
Therefore, the equation of the second line and the answer of numeral a) is

`y=(4)/(5)x-(41)/(5)`

Graphically,