As per given by the question,
There are given that the terminal point,
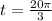
Now,
To find the terminal point, there are use the refrence point,
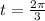
That means,
The given angle is equivalent to the angle ,
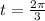
Now,
According to the terminal point concept,
The radius of the unit circle at that point makes a right angle with the coordinates of the terminal point and,
There is also noted that the given terminal is on the 2nd quadrant of the cpordinate axis.
So,
The x value of the terminal point is negative and y value is positive.
Then,
There is use the relation,

Because the radius of the uit circle is 1.
Now,
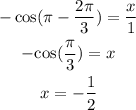
Then,
Similarly to find the y-coordinate.
So,
Here, find the y-coordinate to relate the sine trigonometric function.
![\begin{gathered} \sin (\pi-(2\pi)/(3))=(y)/(1) \\ \sin ((\pi)/(3))=y \\ y=\frac{\sqrt[]{3}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1nzgumx97s8gq30gu2qv113gk5rqzv1dm6.png)
The coordinate of the terminal point is,
![(x,\text{ y)=(-}(1)/(2),\text{ }\frac{\sqrt[]{3}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/i6mgau7f7gwcbo0bb7xnbeg6h0yqp2nbb7.png)
Hence, the option A is correct.