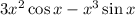Question

Calculate the derivative of x^3cosx

Answer 1

Since g(x) is the product of two terms, we can use the Product Rule to find the derivative.

We essentially have

`g(x)=f(x)\cdot h(x)`

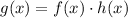
where,

`\begin{gathered} f(x)=x^3\text{ and} \\ h(x)=cosx \end{gathered}`

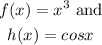
Thus, the Product Rule states that the derivative is equal to:

`f^(\prime)(x)h(x)+f(x)h^(\prime)(x)`

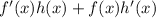
To differentiate f(x), we can use the Power Rule, where the exponent becomes the coefficient, and we decrement the power.

Therefore,

`f^(\prime)(x)=3x^2`

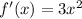
And from our knowledge of derivatives of trig functions

`h^(\prime)(x)=-\sin x`

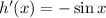
We can now plug these values into the product rule expression to get

`3x^2(\cos x)+x^3(-\sin x)`

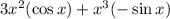
We can rewrite this as

`3x^2(\cos x)-x^3(\sin x)`

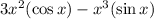
Hence,

`3x^2\cos x-x^3\sin x`

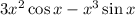
Therefore, the derivative is

`3x^2\cos x-x^3\sin x`