Given:
Circumference of the circle = 832.38 cm
Central angle = 333°
Let's find the length of the arc of the circle.
To find the length of the arc, apply the formula below:

Where:
θ = 333°
2πr = circumference = 832.38 cm
Thus, we have:
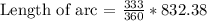
Solving further:
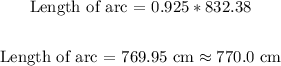
Therefore, the length of the arc of the circle to the nearest tenth is 770.0 cm
ANSWER:
770.0 cm