Question

7. determine which of the lines are parallel and which of the lines are perpendicular

Answer 1

Parallel lines are lines on a plane that never meets. The lines are the same distance apart.

Perpendicular lines form a right angle.

Parallel lines have the same slopes. let's check the slopes of the lines.

`\begin{gathered} \text{ Line p} \\ m_1=(4+1)/(1+4)=(5)/(5)=1 \\ \text{ Line q} \\ m_2=(-1+4)/(3-0)=(3)/(3)=1 \\ \text{ Line r} \\ m_3=(1-4)/(2+2)=-(3)/(4) \\ \text{ line s} \\ m_4=(-2-1)/(1+2)=-(3)/(3)=-1 \\ \text{ line t} \\ m_5=(-4+1)/(0+4)=-(3)/(4) \end{gathered}`

As we can see, the lines that are parallel base on the slopes are as follows

`\begin{gathered} p\parallel q \\ r\parallel t \end{gathered}`

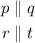
Perpendicular lines, the product of their slopes is equals to negative -1.

`\begin{gathered} m_2m_4=-1 \\ 1*-1=-1 \\ \\ m_1m_4=-1 \\ 1*-1=-1 \\ \\ \end{gathered}`

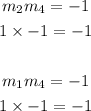
Therefore,

`\begin{gathered} p\perp s \\ q\perp s \\ \end{gathered}`