Question

A 0.33 m tall object is placed 0.31 m from a converging lens with a 0.14 m focal length. How tall is the image?

Answer 1

We know that the lens equation is given as:

`(1)/(f)=(1)/(d_o)+(1)/(d_i)`

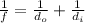
where f is the focal length, do is the distance of the object and di is the distance of the image.

In this case we know:

The focal length is 0.14 m.

The distance of the object is 0.31 m.

Plugging these values in the lens equation we have:

`\begin{gathered} (1)/(0.14)=(1)/(0.31)+(1)/(d_i) \\ (1)/(d_i)=(1)/(0.14)-(1)/(0.31) \\ (1)/(d_i)=(0.31-0.14)/((0.14)(0.31)) \\ d_i=((0.14)(0.31))/(0.31-0.14) \\ d_i=0.255 \end{gathered}`

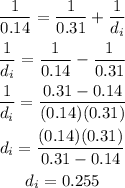
Hence, the distance of the image is 0.255 m.

Now, the magnifying equation states that:

`(h_i)/(h_o)=-(d_i)/(d_o)`

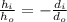
We know that the height of the object is 0.33 m, plugging the values we have:

`\begin{gathered} (h_i)/(0.33)=-(0.255)/(0.31) \\ h_i=-(0.33)((0.255)/(0.31)) \\ h_i=-0.27 \end{gathered}`

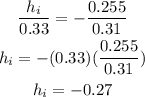
Therefore, the image will be -0.27 m tall. (The minus sign indicates that the image is inverted)