The Solution.
By Similarity Theorem, we have that Trapezoid SUTW is congruent to trapezoid TWVX.
So,
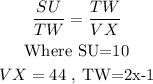
Substituting these values into the ratio above, we get
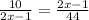
Cross multiplying, we get
![\begin{gathered} (2x-1)^2=44*10 \\ (2x-1)^2=440 \\ \text{Square rooting both sides, we get} \\ 2x-1=\sqrt[]{440} \\ 2x-1=\pm20.976 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9jl5djzvvzwg9i3gfzb2dm0z89yjewhje2.png)
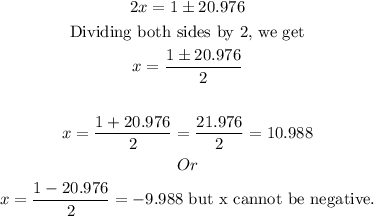
So, the correct value of x is 10.988
To find the length TW:
We substitute 10.988 for x in 2x-1
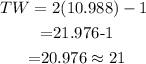
Thus, the correct answer is:
x = 10.988
TW = 20.976