Answer:
The zeros of the given function are 2 and -5. These are the only real zeros.
Step-by-step explanation:
Given the function:
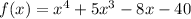
Since (x + 5) is a factor, we are required to find the zeros of the function.
The zeros of the function f(x) are those numbers x, such that when substituted into the given polynomial, results to zero.
The polynomial is of the fourth degree, so it has 4 zeros.
We are given (x+5) to be a factor, we need to divide the polynomial by (x + 5) to obtain the remaining zeros.
Doing this, we have:
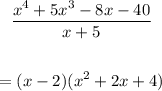
So, the zeros are:

The only real values are:
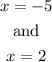
The polynomial
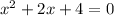
produces values of x that are imaginary.