Question

Complete the square to slove the equation below.x^2 + x = 19/4

Answer 1

Step-by-step explanation

Completing the square allows us to convert and expression like

`x^2+bx`

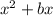
into a square of the form

`(x+c)^2+e.`

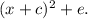
To apply this method, we need to recall first the following identity

`(y+z)^2=y^2+2yz+z^2.`

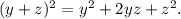
Our task is to take x^2+x and convert it into an expression that looks like the right-hand side of the identity above. On the left, we have x squared; we should then consider x as y in the identity above.

After this square, we have a single x; but we want something like "2yz" there. We only have "y" so far. Multiplying and dividing by 2, we get

`x=2\cdot((1)/(2))\cdot y=2y((1)/(2))\text{.}`

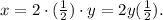
if we set z=1/2, we're done.

Finally, we need to add z^2, which in this case is

`((1)/(2))^2=(1)/(4)\text{.}`

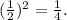
To avoid affecting the expression, we must not only add z^2 but subtract it as well.

In summary, we get

`x^2+x=x^2+2x((1)/(2))+((1)/(2))^2-((1)/(2))^2\text{.}`

And applying the identity, we obtain

`x^2+x=(x+(1)/(2))^2-(1)/(4).`

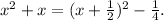
Then, the equation of exercise turns out to be

`(x+(1)/(2))^2-(1)/(4)=(19)/(4)\text{.}`

Let's solve it:

`\begin{gathered} (x+(1)/(2))^2-(1)/(4)=(19)/(4), \\ \\ (x+(1)/(2))^2=(19)/(4)+(1)/(4), \\ \\ (x+(1)/(2))^2=(20)/(4), \\ \\ (x+(1)/(2))^2=5, \\ \\ \sqrt[]{(x+(1)/(2))^2}=\sqrt[]{5},\leftarrow\text{ Taking square root on both sides} \\ \\ |x+(1)/(2)|=\sqrt[]{5},\leftarrow\text{ The square root of a square is the absolute value of what is within the square} \end{gathered}`

Let's solve the absolute value equation:

Answer

The equation of the exercise has two solutions:

`x=\frac{-1+2\cdot\sqrt[]{5}}{2},x=\frac{-1-2\cdot\sqrt[]{5}}{2}\text{.}`