The general equation of a circle is given in the form:
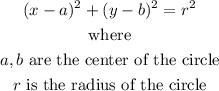
Therefore to go about this, we will follow the steps below
Step 1: write out the equation
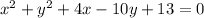
Step 2: Re-goup and apply completing the square method
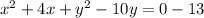
=>
Completeing the square:
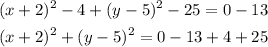
=>
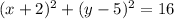
Step 3: Re-write the equation to conform to the general equation
This will give:
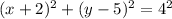
Upon comparing this with the general equation
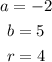
Therefore,
The center = -2, 5
radius = 4