We need to find the percentage of tomato plant that has a height less than or equal to 3.88 feet.
We know that the tomato plant heights are normally distributed with a mean of 3.56 ft and a standard deviation of 0.25 ft.
Thus, the percentage P(x≤3.88) of the heights being less than 3.88 can be calculated using the z-score z, given by:
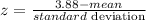
Thus, we have:
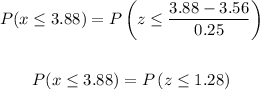
Using a z-score table, we find that:
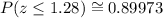
Therefore, the percent we are looking for is:
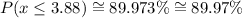
Answer
About 89.97% of tomato plants.