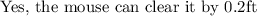a.
Given the equation of the jumps as;
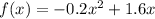
We want to find the range of the jump.To do this let us substitute f(x) = 0 and solve for x;
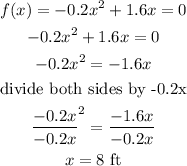
Therefore, the mouse can jump 8 ft horizontally.
b.
We want to know if the mouse can jump over a 3ft fence;
Let's substitute x=8/2 =4 into the equation to get the maximum height the mouse can reach;
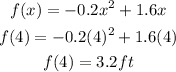
since the maximum height is more than 3ft, it means the mouse can jump higher than 3 ft.
since the maximum height the mouse can jump is 3.2ft, and the fence is 3 ft, the difference between the maximum height and the height of the fence is;
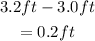
So, the mouse can jump 0.2ft higher than the 3ft fence.
Therefore, the mouse can clear it with 0.2 ft.