The prism of the picture has 5 faces. 2 triangles and 3 rectangles.
The 2 triangles are equal (top and bottom of the prism), with a base of 8cm and a height of 6cm.
The rectangle of the front has a base of 10cm and a height of 13 cm.
The rectangle of the back has a base of 8cm and a height of 13cm.
The rectangle of the left has a base of 6cm and a height of 13cm.
To find the surface area of the prism, we need to find the area of each of those 5 faces, and finally sum them.
The area of the both triangles can be calculated as half the product between base and height:
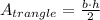
Recalling the dimensions of both triangles (8cm of base and 6cm of height), the area will be:
![A_(trangle)=\frac{(8cm)\cdot(6\operatorname{cm})}{2}=(48)/(2)cm^2=24\operatorname{cm}]()
The area of both triangles is 24 square centimeters. We need to keep in mind that in the final sum we need to add this area twice, since there are 2 triangles.
The area of the front rectangle is just the product between base and height:
![A_(rect-front)=b\cdot h=(10\operatorname{cm})\cdot(13\operatorname{cm})=130\operatorname{cm}]()
The same for the rectangle of the back:
![A_(rect-back)=b\cdot h=(8\operatorname{cm})\cdot(13\operatorname{cm})=104\operatorname{cm}]()
And finally, the same for the left rectangle:
![A_(rect-left)=b\cdot h=(6\operatorname{cm})\cdot(13\operatorname{cm})=78\operatorname{cm}]()
Now we have the area of each of the 5 faces of the prism. To find the surface area we need to sum all of them. Remember the area of the triangle will be added twice:
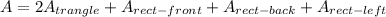
![\begin{gathered} A=2\cdot24\operatorname{cm}+130\operatorname{cm}+104\operatorname{cm}+78\operatorname{cm}^2 \\ A=48\operatorname{cm}+130\operatorname{cm}+104\operatorname{cm}+78\operatorname{cm} \end{gathered}]()
Finally:
![A=360\operatorname{cm}^2]()
The surface area of the prism is 360 square centimeters.