Looking at the function f(x), it is in the factored form, so we can easily find the zeros of the function (that is, the x-intercepts) by equating each factor to zero:
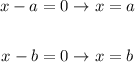
The x-coordinate of the vertex is given by the average value of the zeros:

And the y-intercept can be found by using x = 0:
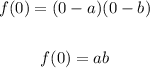
So the graph of this quadratic equation is given by: