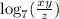Arjun added the logarithm arguments instead of using the properties of the logarithm function to correctly add the three logarithms.
When we add two logarithms that have the same basis, this is equivalent to finding the logarithm of the product of the arguments:
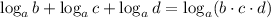
Also, we need to use the following property:
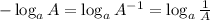
So, for the given expression, the correct solution is:
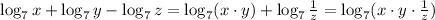
This result can also be written as: