From the given information, we can draw the following picture:
where the widht is three-fourths the length, denoted by x. So, the perimeter (P) is given as
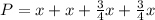
which gives
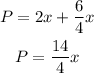
Since the perimeter is 70 feet, we have

so x is given as
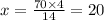
This means that the length measure 20 feet and the width measures:
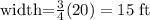
Therefore, the width measures 15 ft.