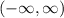Ok, so
We got these two functions:

We're going to find the composition (f o g)(x).
This composition is the same that evaluate the function f(x) in g(x).
This is, f (g(x)):
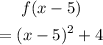
Simplifying:
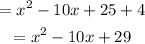
As these two functions are polynomials, then, the domain of (fog)(x), will be: